Funções
Uma função é um bloco de código organizado e reutilizável que é capaz de realizar uma determinada ação. Funções nos ajudam a deixar o nosso código mais modular, trazendo a possibilidade de reusabilidade, conforme nosso programa fica cada vez maior, as funções o tornam mais organizado e gerenciável.
Como vimos ao longo do guia, Python já nos traz várias funções pré-construídas, como por exemplo print() e range(), mas também é possível criarmos nossas próprias funções!
Anatomia das Funções
Podemos imaginar as funções (de modo geral) como um mecanismo capaz de receber valores como input e então realizar operações nesses valores e retornar um output.

Características das Funções
- Possuem um nome
- Possuem parâmetros (0 ou mais)
- Possuem docstrings (opcional, porém recomendado)
- Possuem um corpo
- Retornam algo (opcional)
Definindo uma Função
Em Python devemos seguir a seguinte sintaxe para construirmos uma Função:
def nome_da_função(parametros):"""docstrings"""<comandos>
Para definir uma função é necessário que sigamos algumas regras:
- Bloco de funções começam com a palavra-chave def seguido do nome da função e parenteses ().
- O nome da função identifica exclusivamente a função. A nomenclatura de funções segue as mesmas regras de escrita de identificadores em Python.
- Parâmetros de input ou argumentos (dados fornecidos por nós) devem ser colocados entre parenteses (). Eles são opcionais.
- Dois pontos (
:) para marcar o final do cabeçalho da função. - Opcionalmente podemos usar strings de documentação (docstrings) para descrever o que nossa função faz.
- Uma ou mais instruções Python válidas que constituem o corpo da função. As declarações devem ter o mesmo nível de indentação (geralmente 4 espaços).
- O comando opcional
return (expressão)sai da função, opcionalmente passando um parâmetro para o chamador. O comando de retorno sem argumentos é o mesmo que returnNone.
Por exemplo, vamos definir uma função capaz de converter uma temperatura em Fahrenheit para Celsius.

def fahr_to_celsius(temp):"""Função que recebe como argumento uma temperaturaem Fahrenheit e converte ela para Celsius"""return ((temp - 32) * (5/9))
Uma vez que temos a função definida, agora podemos usá-la. Se quisermos obter ajuda, podemos contar com o comando help() que nos trará o docstrings dessa função.
help(fahr_to_celsius)
Para invocar a função, devemos passar um valor para ela como argumento:
print(fahr_to_celsius(91.76)) # 33.2print(fahr_to_celsius(101.3)) # 38.5
Como essa função tem valor de retorno, podemos armazenar o seu resultado em uma variável:
celsius = fahr_to_celsius(70.76)print(celsius) # 21.53333333333334
Também podemos definir uma função que não irá retornar um valor, por exemplo:
def cumprimentar(nome):"""Essa função cumprimentará a pessoa passada por parâmetro"""print("Olá {0} Seja bem-vindo".format(nome))
A função foi criada e está definida, porém nada aconteceu. Para que ela possa funcionar precisamos invocá-la, para isso chamaremos ela por seu nome e passaremos os parâmetros requisitados por ela:
cumprimentar("Gabriel") # Olá Gabriel Seja bem-vindo
Observe que esta função apenas nos imprime uma string, uma vez que ela não tem valor de retorno.
Parâmetros Padrão
Podemos definir parâmetros padrão para caso a função seja invocada sem nenhum argumento passado, estes preencherão as opções.
def padrao(valor=100):"""Função que apenas imprime um valor"""print("O valor definido foi: " + str(valor))padrao() # 100padrao(10) # 10padrao(33) # 33
Docstring
A primeira string depois do cabeçalho da função é chamada de docstring, é uma string usada para especificar a funcionalidade da nossa função, e embora seja opcional, vos lembro que documentar é uma importante prática de programação, uma vez que possivelmente outras pessoas estarão lendo nosso código, inclusive é importante até mesmo para você lembrar o que você fez!
Caso queiramos ver o docstring de uma função, podemos acessar o atributo __doc__:
print(padrao.__doc__) # Função que apenas imprime um valor
O Comando return
Novamente, o comando return nos permite fazer com que a função retorne um valor e possamos armazená-lo em uma variável, por exemplo:
def func(x):return x + 1y = func(1)z = func(2)print(y) # 2print(z) # 3
Utilizando somente o return, nossa função retornará None:
def func():returnx = func()print(x) # None
Names
Antes de falarmos sobre o conceito de Namespace e Escopo em Python, é importante entendermos os names(também conhecidos como identifiers), que são simplesmente um nome dado aos objetos. Lembre que tudo em Python é um objeto. Names são uma maneira de acessar os objetos.
Por exemplo, quando fazemos a atribuição x = 13, nesse caso 13 é um objeto armazenado em memória e x é o name que este objeto está associado. Nós podemos obter o endereço (em RAM) de um objeto através da função construída em Python chamada id(), vejamos exemplos:
x = 13print(id(13)) # 10914880print(id(x)) # 10914880
Observe que ambos se referem ao mesmo objeto, vamos agora considerar:
x = 13print(f'id(x) = {id(x)}') # id(x) = 10914880x = x + 1print(f'id(x) = {id(x)}') # id(x) = 10914912print(f'id(14) = {id(14)}') # id(x) = 10914912y = 13print(f'id(13) = {id(13)}') # id(13) = 10914880
Veja que inicialmente um objeto 13 é criado e o name x é associado com ele, quando executamos a expressão x = x + 1, um novo objeto 14 é criado, e agora x é associado com esse objeto, tendo ele um novo endereço de memória, podemos confirmar essa afirmação ao verificarmos que id(x) e id(14) possuem o mesmo endereço.
Finalmente, quando executamos y = 13, o novo name y se associa com o objeto antigo 13, obtendo seu endereço.
Essa dinâmica é capaz de tornar Python uma linguagem muito poderosa, uma vez que um name pode referir-se a qualquer tipo de objeto.
x = 1x = 'Programação com Python'x = [0,5,10]
Todas essas expressões são válidas e x irá referir-se à três diferentes tipos de objetos em diferentes instances. Funções também são objetos em Python, sendo assim, um name pode fazer referência a ela.
def zero():return 0z = zeroprint(z()) # 0
O name z definido por nós pode fazer referência a uma função e através dele podemos chamar a função.
Namespace
Um namespace em Python é uma coleção de nomes. Portanto, um namespace é essencialmente um mapeamento de nomes para os objetos correspondentes. A qualquer momento, diferentes namespaces podem coexistir completamente isolados - o isolamento garante que não haja colisões de nomes. Simplesmente, dois namespaces em python podem ter o mesmo nome sem que haja nenhum problema. Um namespace é implementado como um dicionário Python.
No namespace há um mapeamento de nome para objeto, com os nomes como chaves e os objetos como valores. Diversos namespace podem usar o mesmo nome e mapeá-lo para um objeto diferente. Vejamos alguns exemplos de namespaces:
- Namespace Local: Este namespace inclui nomes locais dentro de uma função. Este namespace é criado quando uma função é chamada e dura apenas até que a função retorne.
- Namespace Global: Este namespace inclui nomes de vários módulos importados que você está usando em um projeto. É criado quando o módulo é incluído no projeto e dura até o final do script
- Namespace Built-In: Este namespace inclui funções internas e nomes de exceção internos.
Em Python, você pode então imaginar um namespace como um mapeamento de todos os nomes que você definiu para os objetos correspondentes.
Escopo
Embora existam vários namespaces exclusivos definidos, talvez não possamos acessar todos eles de todas as partes do programa. É nesse momento que o conceito de escopo entra em jogo.
Podemos dizer que o Escopo é a parte do programa a partir do qual um namespace pode ser acessado diretamente sem nenhum prefixo.
A qualquer momento, existem pelo menos três escopos aninhados.
- Escopo da função atual que possui nomes locais
- Escopo do módulo que possui nomes globais
- Escopo externo que possui nomes construídos
Quando uma referência é feita dentro de uma função, o name é procurado no namespace local, depois no namespace global e, finalmente, no namespace externo.
Caso haja uma função dentro de outra função, um novo escopo será aninhado dentro do escopo local.
Consideramos agora o seguinte exemplo:
def externa():z = 13print(z)print(f'valor de z = {z}')def interna():y = 14print(f'valor de y = {y}')interna()x = 10externa()print(f'valor de x = {x}')
O script nos trará o seguinte output:
valor de z = 13valor de y = 14valor de x = 10
Aqui, a variável x está no namespace global. A variável z está no namespace local da função externa() e a variável y está no namespace local aninhado da função interna().
Quando estamos na função interna(), y é uma variável local para nós, z é não-local e x é global. Nós podemos ler e atribuir novos valores à y, porém só podemos ler z e x através da função interna().
Se tentarmos atribuir um novo valor para a variável z, uma nova variável z será criada no namespace local no qual é diferente do não-local z. O mesmo acontece quando atribuimos um novo valor para x.
Entretanto, se declararmos x como global, todas as referências e atribuições irão para a global x. Similarmente, se desejarmos reatribuir a variável z, ela deve ser declarada como não-local, vamos ver mais um exemplo para ilustrar a ideia.
def externa():x = 13print(x)print(f'valor de x = {x}')def interna():x = 14print(f'valor de x = {x}')interna()x = 10externa()print(f'valor de x = {x}')
O script nos trará o seguinte output:
valor de x = 13valor de x = 14valor de x = 10
Neste último script de exemplo, três diferentes variáveis x são definidas em namespaces separados e acessadas de acordo, enquanto que no seguinte script:
def externa():global xx = 20def interna():global xx = 30print(f'x = {x}')interna()print(f'x = {x}')x = 10externa()print(f'x = {x}')
O script nos trará o seguinte output:
x = 30x = 30x = 30
Neste caso específico, todas as referências e atribuições são para a variável global x por causa do uso da palavra-chave global.
O que ocorre então quando chamamos/invocamos uma função?
- Parâmetro formal se conecta com o valor do parâmetro real quando a função é chamada
- Um novo escopo/quadro/ambiente é criado quando entra uma função
- Escopo é o mapeamento de nomes para objetos
# Definição da Funçãodef f(x): # parâmetro formalx += 1print('Em f(x): x = ',x)return x# Código principal do Programa# -> Inicializa a variável x# -> faz uma chamada de função f(x)# -> atribui o retorno da função para a variável zx = 10z = f(x) # parâmetro realprint(z) # 11
Funções como Argumentos
Argumentos podem assumir qualquer tipo, até mesmo funções:
def func_a():print('dentro da func_a')def func_b(y):print('dentro da func_b')return ydef func_c(z):print('dentro da func_c')return z()print(func_a()) # chama a função func_a, não recebe parâmetrosprint(5+func_b(2)) # chama a função func_b, recebe um parâmetroprint(func_c(func_a)) # chama a função func_c, recebe outra função como parâmetro
Observe que:
- A função
func_aretornaNone, pois ela apenas imprime uma string - A função
func_bretorna2(valor que passamos via argumento) - A função
func_crecebe afunc_acomo parâmetro, que por sua vez retornaNone
Exemplo do Escopo
Nem todas as variáveis são acessíveis a partir de todas as partes do nosso programa, e nem todas as variáveis existem durante o mesmo período de tempo. Onde uma variável é acessível e por quanto tempo ela existe depende de como é definida. Chamamos a parte de um programa onde uma variável está acessível de seu escopo, e a duração para a qual a variável existe seu tempo de vida.
Uma variável que é definida dentro de uma função é local para essa função. Ela é acessível a partir do ponto em que foi definida até o final da função e existe enquanto a função estiver em execução. Os nomes dos parâmetros na definição da função se comportam como variáveis locais, mas contêm os valores que passamos para a função quando a chamamos. Quando usamos o operador de atribuição (=) dentro de uma função, seu comportamento padrão é criar uma nova variável local - a menos que uma variável com o mesmo nome já esteja definida no escopo local.
- Dentro de uma função, podemos acessar uma variável definida fora dela
- Dentro de uma função, não podemos modificar uma variável definida fora dela, na verdade podemos utilizando a variável global, mas normalmente não é o ideal
def f(y):# x é redefinido no escopo de fx = 1x += 1print(x)x = 5f(x) # 2print(x) # 5
Neste caso temos diferentes objetos x, a função f() irá utilizar o x definido dentro dela e print() irá imprimir o objeto x global.
def g(y):print(x)print(x+1)x = 5g(x)print(x)# 5# 6# 5
Neste caso a função g() e print() vão usar o mesmo objeto x global.
def h(y):x += 1x = 5h(x)print(x)# UnboundLocalError: local variable 'x' referenced before assignment
Neste exemplo ocorrerá um erro, uma vez que a função h() está tentando modificar o objeto x antes mesmo dele ser definido.
A Função globals()
Como o próprio nome indica, a função globals() exibirá informações de escopo global. Por exemplo, se abrirmos um console Python e inserirmos globals(), um dicionário incluindo todos os nomes e valores de variáveis no escopo global será retornado.
Veja que estou usando ... para abreviar o resultado:
>>> globals()# {'__name__': '__main__', ..., '__builtins__': <module 'builtins' (built-in)>}
Se adicionarmos uma variável, ela agora será incluída no escopo global:
x = 1globals()# {'__name__': '__main__', ..., '__builtins__': <module 'builtins' (built-in)>, 'x': 1}
A Função locals()
Como o próprio nome indica, a função locals() retornará um dicionário incluindo todos os nomes e valores locais.
def anime():nome = 'Naruto'print(locals())anime() # {'nome': 'Naruto'}
Se chamarmos a função locals() no escopo global, o resultado será idêntico ao resultado da função globals(), portanto esteja ciente disso quando usá-la:
globals() is locals() # True
*args & **kwargs
As variáveis mágicas *args e **kwargs são normalmente usadas em definições de funções, elas nos permitem passar um número variável de argumentos para uma função. Variável nesse caso significa que não sabemos de antemão quantos argumentos vamos receber, então nesse caso utilizamos *args e **kwargs.
*args
*args é usado para enviar uma variável que não tenha palavras-chave, veja um exemplo:
def soma(*args):total = 0for num in args:total += numreturn totalprint(soma(2,3,4,6)) # 15print(soma(2,3,4,6,5,5,5,1,2)) # 32print(soma(2,3)) # 5
**kwargs
**kwargs nos permite passarmos variáveis com palavras-chave como argumento, veja exemplos:
def pessoa(**kwargs):print(kwargs)for nome, idade in kwargs.items():print(f'{nome} tem atualmente {idade} anos de idade')pessoa(gabriel='33', rafael='47', daniel='22')# {'gabriel': '33', 'rafael': '47', 'daniel': '22'}# gabriel tem atualmente 33 anos de idade# rafael tem atualmente 47 anos de idade# daniel tem atualmente 22 anos de idade
Recursão
'Recursividade' é um termo usado de maneira mais geral para descrever o processo de repetição de um objeto de um jeito similar ao que já fora mostrado. Um bom exemplo disso são as imagens repetidas que aparecem quando dois espelhos são apontados um para o outro.
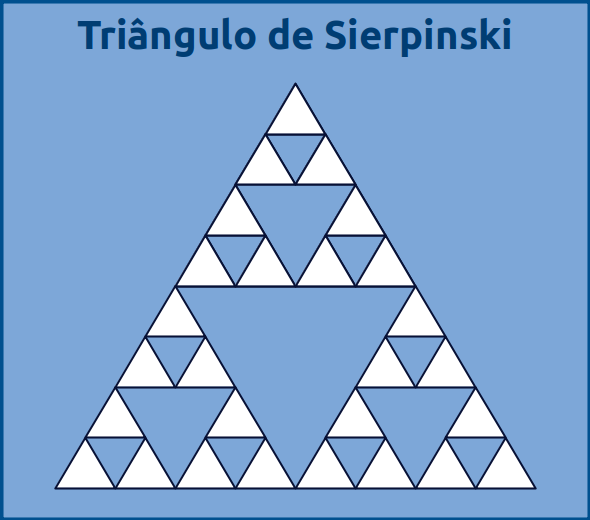
Outro grande exemplo seria O Triângulo de Sierpinski - também chamado de Junta de Sierpinski - é uma figura geométrica obtida através de um processo recursivo. Ele é uma das formas elementares da geometria fractal por apresentar algumas propriedades, tais como: ter tantos pontos como o do conjunto dos números reais; ter área igual a zero; ser auto-semelhante (uma parte sua é idêntica ao todo); não perder a sua definição inicial à medida que é ampliado. Foi primeiramente descrito em 1915 por Waclaw Sierpinski (1882 - 1969), matemático polonês.
Imagem do Triângulo de Sierpinski:
Pensando de forma computacional:
Algoritmicamente falando, Recursão é uma maneira de desenvolver soluções para problemas através de divide-and-conquer ou decrease-and-conquer, reduzindo o problema para versões simplificadas do mesmo problema
Semanticamente: Uma técnica de programação onde a função chama a si mesmo
Em Programação, o objetivo é não ter recursão infinita
Deve-se ter 1 ou mais casos bases que são fáceis de resolver
Deve-se resolver o mesmo problema em algum outro input com o objetivo de simplificar o input do problema maior
Recursão em Python
Nós sabemos que em Python é possível uma função chamar outras funções, inclusive é possível que uma função chame ela mesma, esses tipos de constructos são chamados de funções recursivas.
A seguir temos o exemplo de uma função que descobre o fatorial de um inteiro. Fatorial de um número é produto de todos inteiros de 1 até esse número. Por exemplo, o fatorial de 5 (denotado por 5!) é 1x2x3x4x5 = 120.
Exemplo de uma função recursiva:
def fatorial(x):"""Essa é uma função recursivaEla calcula o fatorial de um número inteiro"""if x == 1:return 1else:return (x * fatorial(x - 1))y = 4z = 10print("O fatorial de {0} é {1}".format(y,fatorial(y))) # O fatorial de 4 é 24print("O fatorial de {0} é {1}".format(z,fatorial(z))) # O fatorial de 7 é 3628800
No exemplo acima fatorial() é considerada uma função recursiva, pois chama a ela mesma. Quando nós chamamos essa função com um inteiro positivo, ela chamará recursivamente ela mesma diminuindo o número. Para entendermos melhor, veja o cálculo que ocorre:
fatorial(4) # Primeira chamada com 44 * fatorial(3) # Segunda chamada com 34 * 3 * fatorial(2) # Terceira chamada com 24 * 3 * 2 * fatorial(1) # Quarta chamada com 14 * 3 * 2 * 1 # Retorno da quarta chamada, uma vez que y = 14 * 3 * 2 # Retorno da terceira chamada4 * 6 # Retorno da segunda chamada24 # Retorno da primeira chamada
Como podem ver, nossa recursão acaba quando o valor de y reduz a 1, essa é considerada a condição base. Toda recursão deve ter uma condição base que para a recursão ou a função ficará chamando-a eternamente.
Recursão com Múltiplos Casos Base
Como já vimos, um caso de base é um cenário de encerramento que não usa recursão para produzir uma resposta, podemos ter um ou mais desses cenários em nossas funções.
Na matemática, a Sucessão de Fibonacci (ou Sequência de Fibonacci), é uma sequência de números inteiros, começando normalmente por 0 e 1, na qual, cada termo subsequente corresponde à soma dos dois anteriores. A sequência recebeu o nome do matemático italiano Leonardo de Pisa.
Fibonacci modelou o seguinte desafio:
- Pares de coelhos recém-nascidos (um macho e uma fêmea) são colocados em um curral
- Coelhos se acasalam na idade de um mês
- Coelhos tem um mês de período de gestação
- Assumindo que o coelho nunca morre, a fêmea sempre produz um novo par (um macho e uma fêmea) a cada mês a partir do segundo mês
- Quantos coelhos fêmeas estão lá no final do ano?
Fibonacci em Python
Vamos então definir o problema, para que seja mais fácil solucioná-lo:
- Depois de um mês (chamamos ele de 0) = 1 fêmea
- Depois do segundo mês, ainda 1 fêmea (agora grávida)
- Depois do terceiro, 2 fêmeas, 1 grávida, 1 não-grávida
- Em geral, temos então
fêmeas(n) = fêmeas(n-1) + fêmeas(n-2)- Cada fêmea viva no mês
n-2irá produzir uma fêmea no mêsn - Estes podem ser adicionados aqueles vivos no mês
n-1para obter total vivos no mêsn
- Cada fêmea viva no mês
Temos então os seguintes casos:
- Casos Base: - Femeas(0) = 1 - Femeas(1) = 1
- Caso Recursivo - Femeas(n) = Femeas(n-1) + Femeas(n-2)
Convertendo para a linguagem Python:
def fib(x):"""Assume x como inteiro >= 0Retorna o Fibonacci de x"""if x == 0 or x == 1:return 1else:return fib(x-1) + fib(x-2)print(fib(8)) # 34print(fib(10)) # 89
Vantagens e Desvantagens
Vantagens da Recursão:
- Funções recursivas tornam o código limpo e elegante
- Uma tarefa complexa pode ser quebrada em sub-problemas usando a recursão
- Gerar sequências é mais fácil com recursão
Desvantagens da Recursão:
- As vezes a lógica por trás dela pode ser complexa de entender
- Chamadas recursivas são custosas e ineficientes e podem nos custar muita memória e tempo!
- Funções recursivas são mais difíceis de debugar (processo de encontrar e reduzir defeitos de um programa).
Por fim, entendemos que as funções são um tema essencial e fundamental para a programação, elas são capazes de facilitar muito a vida dos programadores através da abstração, tornando os códigos muito mais elegantes, modulares e fáceis de entender. O código ainda pode ser utilizados muitas vezes e precisa ser debuggado/testado apenas uma vez.
Cheque a documentação oficial do Python para conhecer todas as funções construídas no interpretador Python.